Soluciones de Soft Computing
ITCL ofrece distintas soluciones de Soft Computing, el cual se centra en la incorporación de aprendizaje automático en sistemas híbridos, análisis de datos, selección de características, modelado de sistemas, clasificación y optimización de sistemas. También, se incluyen soluciones para el tratamiento de sistemas bioinformáticas, clusterización, clasificación y modelado de series dinámicas aplicadas a perfiles de expresión genética.
Soft Computing para la clasificación de series dinámicas aplicadas a perfiles de expresión genética
Sot Computing de diseño propio que engloba diferentes algoritmos propios para la agrupación de genes coexpresados en microarrays de análisis de datos (MDA). Adecuado, para el uso de investigadores, que traten determinar los genes importantes y las relaciones co-expresadas entre ellos, para grandes conjuntos dinámicos de datos, de modo que se permita optimizar una característica de salida.
Algunos de los algoritmos diseñados que integra el software son:
- Shape Index (SC). Agrupación sin tener en cuenta la salida de cada muestra.
- Output Shape Index (SOC). Agrupación teniendo en cuenta la correlación del gen con la salida.
- Dynamic Shape Index (DSC). Versión dinámica del método SC.
- Output Dynamic Shape Index (DSOC). Versión dinámica cel método SOC.
- Relaxed Shape Index (RSC). Ampliación del método SOC
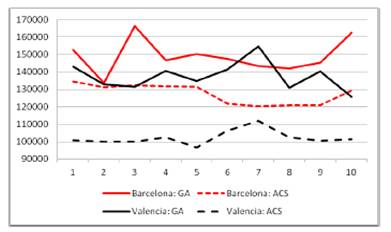
El software integra métodos de fusión que combinan en una única agrupación las agrupaciones creadas a partir de cada una de las series temporales de los datos de microarrays realizadas de forma independiente. La detección de los clusters más importantes dentro de los posibles se realiza usando diferentes medidas sobre los genes, entre las que destacan el Coeficiente de Correlación de la Información (ICC), Coeficiendo de Correlación de Pearson (PCC) y las medidas Shape Increase.
Optimización de variables de máquina a partir del modelo
Sistemas de Soft Computing de diseño propio, para la optimización de parámetros de máquina en procesos de fabricación incluyendo el desarrollo de modelos para evaluar el comportamiento de las variables de la máquina en el proceso y, para encontrar la función de aptitud a optimizar.
Este proceso se realiza en primer lugar mediante la obtención de la función objetivo paramétrica o de caja negra del sistema a optimizar. Posteriormente la optimización de los parámetros de la máquina se lleva a cabo mediante Algoritmos Genéticos mono–objetivo y multi-objetivos, recocido simulado, o colonias de hormiga.
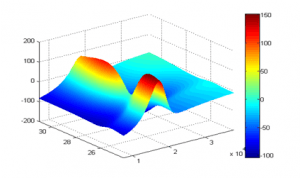
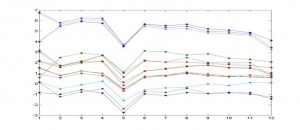
Un ejemplo de las búsquedas de los objetivos sobre un sistema de fabricación con tres objetivos se presenta a continuación.
-
- Gráfico 3-D. El eje x representa una entrada, el eje Y otra entrada a optimizar y el eje Z la salida.
-
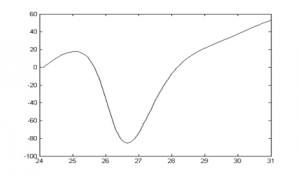
- Gráfico 2-D. El eje x representa una entrada y el eje Y la salida.
-
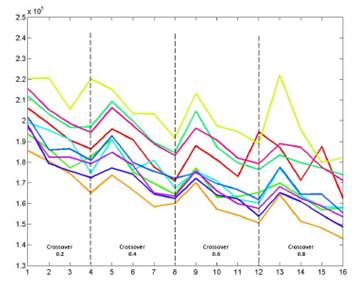
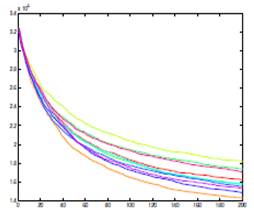
- Gráficos 3-D. Resultado de una búsqueda multi-objetivo
Sistemas de optimización de enrutamiento de vehículos
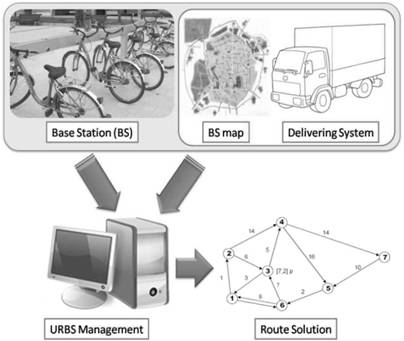Diseño de diferentes algoritmos evolutivos híbridos de planificación de rutas para varios vehículos, minimizando los costes asociados al transporte, como puede ser: minimizar el tiempo total de transporte, minimizar la distancia total recorrida, minimizar el tiempo de espera, minimizar los vehículos a utilizar, etc. Todo ello satisfaciendo una serie de múltiples restricciones y limitaciones.
Elementos principales:
- Clientes/puntos de entrega o recogida
- Almacén/Almacenes
- Flota de vehículos (capacidad de cada uno)
- Red de transporte
- Función a minimizar
Modelado:
Modelación de los problemas de optimización como diferentes tipos de VPR (Vehicle Routing Problem):
- VRP with Pickup and Delivery (VRPPD): algunos clientes representan lugares de recogida y otros representan lugares de entrega.
- VRP with Time Windows (VRPTW): los clientes tienen ventanas de tiempo en las que tienen que ser atendidos.
- Capacitated VRP (CVRP): los vehículos tienen capacidad limitada.
- Distance-Constrained VRP (DVRP): longitud máxima permitida para una ruta.
- Multiple Depot VRP (MDVRP): múltiples almacenes para suministrar a los clientes.
Dado que VRP es un problema de optimización combinatorio complejo (NP-hard) se han desarrollado diferentes técnicas heurísticas para resolver los diferentes VRPs: Algoritmos Genéticos, Inteligencia de Enjambre y Sistemas de Colonias de Hormigas.
